Boolean Laws
There are six types of Boolean Laws.
Commutative law
Any binary operation which satisfies the following expression is referred to as commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.
Associative law
This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.
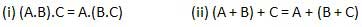
Distributive law
Distributive law states the following condition.
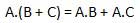
AND law
These laws use the AND operation. Therefore they are called as AND laws.
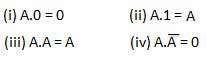
OR law
These laws use the OR operation. Therefore they are called as OR laws.
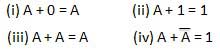
INVERSION law
This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.
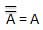
De Morgan's Theorems
De Morgan has suggested two theorems which are extremely useful in Boolean Algebra. The two theorems are discussed below.
Theorem 1
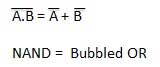
The left hand side (LHS) of this theorem represents a NAND gate with inputs A and B, whereas the right hand side (RHS) of the theorem represents an OR gate with inverted inputs.
This OR gate is called as Bubbled OR.
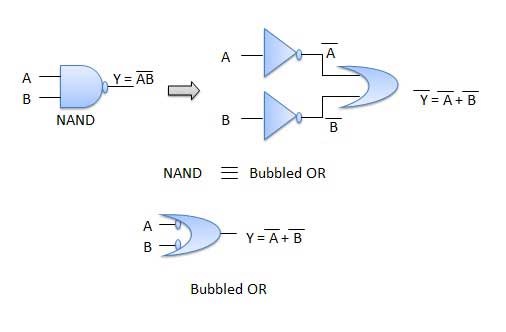
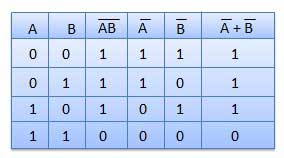
Table showing verification of the De Morgan's first theorem −
Theorem 2
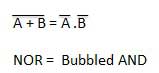
The LHS of this theorem represents a NOR gate with inputs A and B, whereas the RHS represents an AND gate with inverted inputs.
This AND gate is called as Bubbled AND.
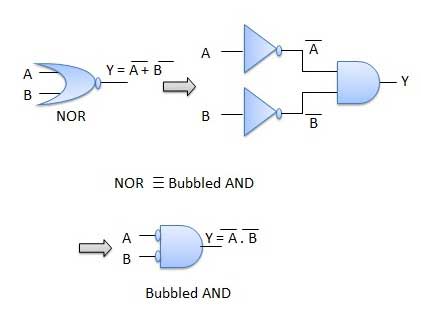
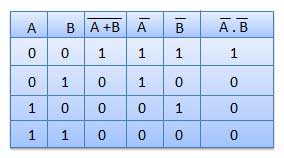
Table showing verification of the De Morgan's second theorem −
Applications of De Morgan’s Theorems and Boolean Laws
Circuit Simplification: De Morgan’s theorems help simplify complex logic circuits by transforming AND gates into OR gates (or vice versa) and minimizing the use of NOT gates.
Logic Gate Design: These theorems are crucial when designing and optimizing digital circuits using NAND or NOR gates, which are the building blocks of many circuits.
Programming: In software development, Boolean laws are used to optimize conditional statements, improve code efficiency, and reduce complexity.
Error Detection: By applying these laws, it's easier to detect and correct logical errors in Boolean expressions or circuit designs.
0
Post a Comment
Do leave your comments.